Calculating the present value of perpetuity can be complex, but our Present Value of Perpetuity Calculator simplifies this task. In this article, we’ll explore how to accurately determine the present value of perpetuity.
What is Perpetuity?
Perpetuity, as its name suggests, is a financial term that describes an infinite series of uniform cash flows. While the idea of “forever” payments may sound like something from a fantasy novel, perpetuity has played a vital role in finance and history.
The Basics of Perpetuity
At its core, perpetuity refers to a stream of cash flows that never ends. When you compare this to an annuity – which also provides a series of payments – the difference is clear: annuities have an end date, but perpetuities do not. For example, if you were to receive $100 every year indefinitely, that would be a perpetuity. If you were to receive $100 every year for 10 years, that would be an annuity.
Historical Significance
One cannot discuss perpetuities without mentioning the British consols. Introduced in the 18th century, these were government-issued bonds that promised the holder an unending annual interest payment. Essentially, by purchasing a consol, the investor lent money to the government and, in return, received interest payments indefinitely. The principal was never repaid, only the interest. These consols were a testament to the British government’s creditworthiness and its ability to manage long-term obligations.
Although the British consols were redeemed and phased out in the 21st century, specifically in 2015, they remain a striking illustration of the concept of perpetuity in practical use.
Modern Relevance
While true perpetuities are rare in today’s financial markets, the concept itself is still significant. It’s foundational in understanding various financial theories and models, especially when evaluating stocks, bonds, or valuing certain types of businesses. Additionally, the concept helps finance students and professionals grasp the essential idea of the time value of money.
Present Value of Perpetuity Formula
You might wonder how an infinite series of cash flows can have a finite present value. The answer lies in the diminishing impact of each subsequent payment due to the time value of money. In simpler terms, a dollar today is worth more than a dollar in the future due to factors like inflation and opportunity cost. Therefore, the payment in the very remote future may be worth nothing in the present.
The formula for the present value of a single future cash flow C at a discount rate r received t years from now is:
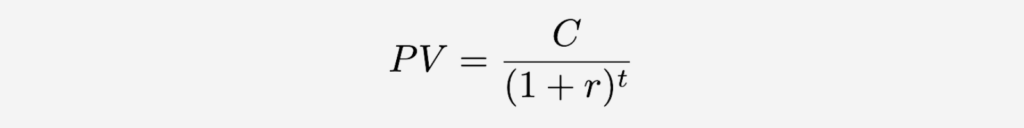
In a perpetuity, you’ll receive C one year from now, C two years from now, and so on, indefinitely. So, the present value of perpetuity would be the sum of all these discounted cash flows:
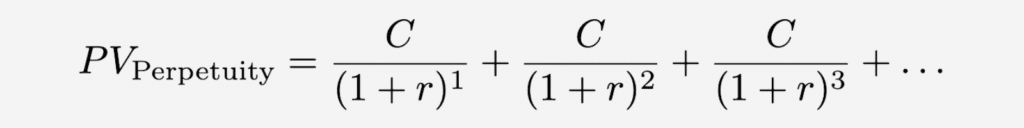
This is an infinite geometric series where the first term a=C/(1+r), and the common ratio b=1/(1+r).
The sum S of an infinite geometric series is given by:
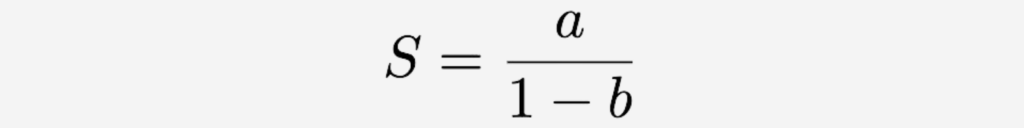
Substituting the values for a and b into this equation, we get:
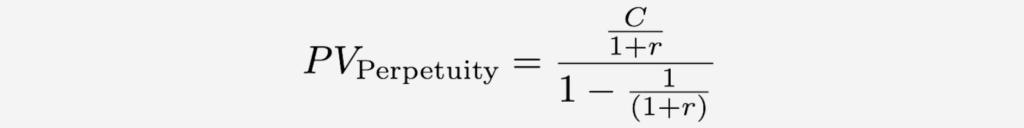
Simplifying this equation leads to the commonly used formula for the present value of perpetuity:

Factors Influencing Present Value of Perpetuity
Several factors can significantly influence the “present value of perpetuity,” making understanding their impact when involved in financial transactions crucial. At the heart of this valuation are two primary components: the constant annual cash flow C and the discount rate r. Let’s delve deeper into their significance and the external factors that play a pivotal role in shaping them.
Constant Annual Cash Flow (C)
The constant annual cash flow is essentially the amount one anticipates receiving every year. When this amount is larger, the present value of the perpetuity will naturally be higher. For instance, two properties in different neighborhoods might offer different rental incomes due to location, amenities, or demand. A property that assures a higher annual rent will possess a greater present value, assuming other factors remain the same.
Discount Rate (r)
Then comes the discount rate, a crucial component in determining the present value. It essentially represents both the time value of money and the associated risks of the investment.
When you have higher prevailing interest rates in the economy or when the particular investment is deemed riskier, the discount rate goes up. The consequence of a higher discount rate is a decrease in the present value of the perpetuity. Conversely, in a more stable economic environment or with safer investments, the discount rate might be lower, boosting the present value.
Inflation
One cannot discuss the discount rate without considering inflation. Inflation, the general rise in prices over time, diminishes the purchasing power of money.
When inflation is expected to be high in the future, the real value of future cash flows decreases. As a direct consequence, the discount rate used to value these cash flows tends to increase, leading to a reduced present value of perpetuity.
Risk Profile
Another essential aspect to consider is the risk profile associated with the cash flows. No two investments are alike. Some might promise steady returns with minimal fluctuations, while others might be fraught with uncertainties.
An investment in a well-established, stable industry might have less associated risk than an investment in a nascent, volatile sector. Consequently, the riskier the anticipated cash flows, the higher the discount rate applied, which in turn reduces the present value.
Present Value of Perpetuity Calculation Example
Let’s step into the shoes of an astute investor evaluating the purchase of a rental property. This property has an attractive promise: a consistent annual income of $10,000. To make an informed decision, the investor must ascertain the present value of this perpetual income stream. The Present Value of Perpetuity Calculator becomes a valuable tool in this endeavor.
Let’s break down the process of using the calculator:
The investor starts by keying in the expected annual income from the rental property into the calculator. In our scenario, this is $10,000. This figure essentially captures the property’s capacity to generate cash year after year.
Following this, the investor needs to incorporate the current market discount rate, reflecting the prevailing economic conditions and the risk profile of such an investment. Given that similar properties in the market have a discount rate of 5%, this percentage is entered into the calculator. The discount rate serves as a window to peer into the future and determine how future cash inflows fare against present-day dollars.
With both these values fed into the calculator, all that remains is to initiate the computation. Upon clicking the ‘Calculate’ button, the magic unfolds. The calculator promptly evaluates the present value, yielding a result of $200,000 for our hypothetical rental property. This figure provides valuable insight: to achieve the targeted return on investment, given the perpetual cash flow and the prevailing market conditions, our investor should consider a purchase price of up to $200,000 for the property.
The Limitation of the Present Value of Perpetuity Model
The allure of the present value of perpetuity model is unmistakable; its simplicity provides a streamlined approach to understanding the value of endless cash flows in today’s terms. However, a discerning financial mind must also appreciate the inherent boundaries and potential pitfalls that come with the model’s assumptions.
One primary constraint of the model is its foundational premise: that cash flows remain unchanged throughout time. In the intricate dance of the financial world, factors such as inflation, tumultuous market dynamics, and evolving industry landscapes constantly reshape the trajectory of cash inflows. For instance, a booming business today might face technological obsolescence in a decade, thereby altering its earnings potential. When the model is applied to such dynamic entities, its projection might paint an overly optimistic or pessimistic picture.
Moreover, the perpetuity model, by definition, visualizes an unending timeline, a scenario that often finds little resonance in the real business landscape. The word ‘forever’ is a romantic notion, but in the pragmatic world of finance, very few entities endure eternally. Companies, irrespective of their current success, might face unforeseen challenges that threaten their very existence. Similarly, financial instruments such as bonds have defined maturities, making the infinite horizon of perpetuity misaligned with their actual life span.
Another subtle yet significant aspect to ponder is the rigidity of the discount rate used in the model. The discount rate encapsulates both the prevailing economic climate and the specific risk profile of the investment. However, both these factors are fluid. Economic downturns, policy changes, or shifts in investor sentiment can all influence this rate, rendering previous calculations obsolete.
Final Words
The present value of perpetuity calculator provides quick and precise insights into understanding the present value of an endless stream of cash flows. Yet, like all tools, its efficacy is only as good as the user’s awareness of its boundaries. The present value of perpetuity model is undeniably powerful, but its full potential is unlocked when one acknowledges its constraints. By discerning when and where to use this model—and keeping its limitations in mind—one can truly harness its rich insights while maintaining accuracy.









